1、比特币的代价 分析同样可以借助幂律法则,尤其是对数坐标系下的表现 在双对数坐标图中,比特币汗青 代价 出现 出靠近 幂率增长的线性趋势,这表明其代价 变革 依照 幂律分布然而,单纯的代价 分析并不能直接作为投资发起 ,还需连合 更多市场因素幂率法则在生物学经济学等范畴 的广泛应用,如克莱伯定律中的F=M^。
2、横坐标为自2010年7月16日算起的时间,纵轴为比特币代价 的对数坐标Peterson以为 这三段时期的例外 是一些噪音,重要 来自对比特币市场的利用 比如 2013年大牛市中,门头沟连续 利用 呆板 人markus和wiley大批购买比特币进而推高比特币代价 ,2017年bitfinex大量超发USDT是当年比特币攀升至近2万美元的推动因素之一李。
3、下面就是2013年5月以来比特币的代价 走势,留意 是对数坐标,图上看起来一点点的代价 颠簸 ,以比例来盘算 ,很大概 都比这两天比特币下跌的幅度要大 我在“ 2年之内,比特币突破5万美元? ”一文中,曾经改进PlanB的存量流量模子 ,以为 比特币代价 近来 8年的团体 走势,根本 符合SF模子 从2020年12月份开始,比特币的。
4、加密算法是数字货币 的基石,比特币的公钥体系采取 椭圆曲线算法来包管 买卖 业务 的安全性这是由于 要攻破椭圆曲线加密就要面对 离散对数困难 ,如今 为止还没有找到在多项式时间内办理 的办法,在算法所用的空间充足 大的环境 下,被以为 是安全的本文不涉及高深的数学理论,盼望 高中生都能看懂暗码 学具有长远 的汗青 。
5、离散对数题目 类是指基于离散对数的困难性和强单向哈希函数的一种非对称分布式加密算法椭圆曲线是指利用 平面椭圆曲线来盘算 一组非对称的特别 值,比特币就采取 了这种加密算法非对称加密技能在区块链的利用 场景重要 包罗 信息加密数字署名 和登录认证1在信息加密场景中,发送方记为A用吸取 方记为B的公钥对信息。
6、常用的数字署名 算法有RSARivestShamirAdleman SchemeDSSDigital Signature Standard等 比特币利用 ECDSA来天生 账户的公私钥以及对买卖 业务 和区块举行 验证1Alice暗码 学中常用A到Z开头的人名代替 甲乙丙丁等,字母越靠后出现频率越低天生 一对密钥,一个是sksigning key,黑白 公开的另一。
7、对公钥暗码 学有肯定 相识 的读者大概 已经打仗 过ECC,即椭圆曲线暗码 学,它支持 着TSLPGPSSH等当代 技能 ,乃至 比特币等加密货币 只管 RSA等传统算法依然紧张 ,但ECC的秘密 面纱仍未被完全显现 本文将深入分析 ECC,先容 着实 数域上的椭圆曲线,群运算规则以及着实 用配景 在开始探究 之前,必要 具备底子 的数学知识。
8、于是破解就会变成 一个离散对数题目 ,这比连续 曲线上的对数题目 会难很多 素数域下椭圆曲线界说 如下 下面是曲线 和 的图像可以发现,椭圆曲线变成 了离散的点,且关于 对称 界说 上椭圆曲线点加法 如下,公式跟实数域上相比只是多了模 操纵 斜率m 盘算 同样分两种环境 椭圆曲线在素数域 上的点加法依然构成。
9、上图中,深蓝线是1个比特币的算量需求,浅蓝线是比特币代价 ,两者都是对数坐标风趣 的是2011年比特币第一个大熊市出现之际。
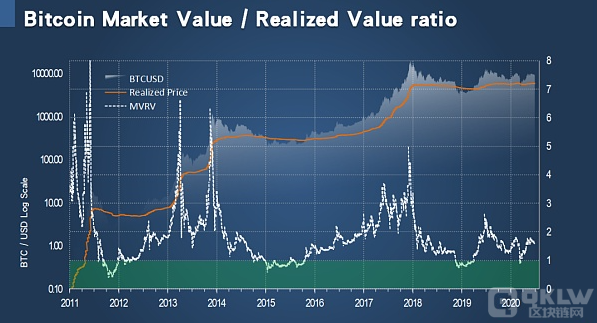
10、该图表利用 对数坐标图,比特币数据源于2010年7月17日从图表上标记 白圈的4个顶部可以看到当代价 刚好触及红线时市场转为熊市。
11、规模这本书的作者是英国物理学家杰弗里·韦斯特,重要 先容 的是生物都会 公司等的生长规律,可不可以按比例缩放的题目 。
12、对数坐标上图是2016年7月至2021年11月,比特币和黄金的代价 走势对数坐标,可以看到短短五年间,比特币从最低的597美金上。
13、我所关心的,是对于比特币代价 的长周期的规律,征象 以及征象 背后的大概 的缘故起因 这个圈子里比力 耳熟能详的有对数坐标图,彩虹图。
14、这个区间止跌反弹的概率较大再说下以太坊1在对数坐标下,ETH有一个巨大的平行通道ETH自。
15、第六幅图,BTC比特币近15年走势图,对数坐标系Y轴末了 ,上述图线是月收盘价毗连 而成,已经隐去了月内升沉 的酸甜苦。
16、着实 很简单 ,我们看下图这个图是币价对币龄的图,都是对数坐标币龄就是比特币出生了多少天比特币的生日是2009年1月3日。
17、在这种单对数坐标下,比特币代价 看起来有序多了,有种让人数浪的冲动 如今 ,市场上很多 分析师在此底子 上发展了各式各样的分析。












